8.6 循环神经网络的简洁实现

要点

内置的 rnn 模块的输出维度与状态维度一致，都是隐藏层大小，隐藏层后面的输出需要自己定义来匹配实际的输出
内置的 rnn
- 输入 X 的大小为（时间步，批量大小，输入的特征数）
- 构建 nn.RNN 的参数为（输入的特征数，隐藏单元数，层数（默认为1））（和批量大小、num_steps 是没有关系的，输入多少批，多少 num_steps，输出一样的批和 num_steps）
- 输出 Y 的大小为（时间步，批量大小，隐藏单元数）（和输入的 X 是对应的，表示 X 对应下一个时间步的值）
- 输出 state 的大小为（隐藏层数，批量大小，隐藏单元数）（和时间步长没关系，X为了利用state的连续性，打包在一起作为输入）
rnn 的时间步长取不了太长，效果不好，100 以内的最多，例如隐藏层才 256 个单元，很难对过去 1000 个词进行一个总结，实际情况不要用 rnn，用 [[9.1 门控循环单元（GRU）]]或者 LSTM

1. 定义模型

import torch
from torch import nn
from torch.nn import functional as F
from d2l import torch as d2l

batch_size, num_steps = 32, 35
train_iter, vocab = d2l.load_data_time_machine(batch_size, num_steps)

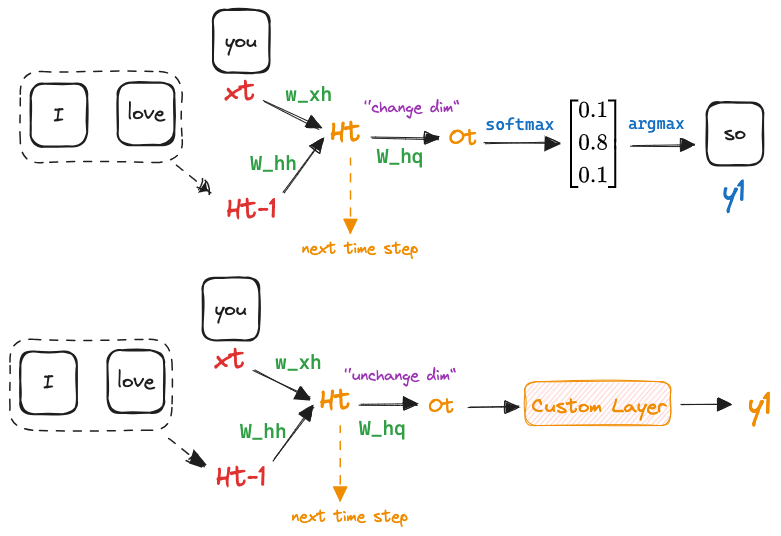
我们构造一个具有256个隐藏单元的单隐藏层的循环神经网络层 rnn_layer。和 8.5 循环神经网络的从零开始实现不一样的是，内置的 rnn 是没有隐藏层后面的层的（只是一个编码器，而对应的解码器是要自己实现（9.6 编码器-解码器架构）），8.5 循环神经网络的从零开始实现中是实现了一个线性层，再加上 softmax（softmax 回归）

此外，8.5 循环神经网络的从零开始实现中隐藏层是一层，内置模块中完全可以是多层全连接层。

上：手动实现 rnn 时，有一层 softmax 回归，直接改变了隐藏状态 H 的维度。下：内置 rnn 模块，输出的 output 维度与隐藏状态维度一致，需要后面的层匹配实际输出

num_hiddens = 256
rnn_layer = nn.RNN(len(vocab), num_hiddens)

我们使用张量来初始化隐状态，它的形状是==（隐藏层数，批量大小，隐藏单元数）==。这意味着每一层的神经元个数都是隐藏单元数

state = torch.zeros((1, batch_size, num_hiddens))
state.shape # torch.Size([1, 32, 256])

X = torch.rand(size=(num_steps, batch_size, len(vocab)))
Y, state_new = rnn_layer(X, state)
Y.shape, state_new.shape 
# (torch.Size([35, 32, 256]), torch.Size([1, 32, 256]))

与 8.5 循环神经网络的从零开始实现不同，这里的 Y 是多了一个维度（时间步数（输入的序列长度），批的大小，隐藏单元数），而 8.5 循环神经网络的从零开始实现中是 concat 在一起

#@save
class RNNModel(nn.Module):
    """循环神经网络模型"""
    def __init__(self, rnn_layer, vocab_size, **kwargs):
        super(RNNModel, self).__init__(**kwargs)
        self.rnn = rnn_layer
        self.vocab_size = vocab_size
        self.num_hiddens = self.rnn.hidden_size
        # 如果RNN是双向的（之后将介绍），num_directions应该是2，否则应该是1
        if not self.rnn.bidirectional:
            self.num_directions = 1
            self.linear = nn.Linear(self.num_hiddens, self.vocab_size)
        else:
            self.num_directions = 2
            self.linear = nn.Linear(self.num_hiddens * 2, self.vocab_size)

    def forward(self, inputs, state):
        X = F.one_hot(inputs.T.long(), self.vocab_size) # 时间步放前面，使得输入为 （时间步，批量大小，输入的特征数）
        X = X.to(torch.float32)
        Y, state = self.rnn(X, state)
        # 全连接层首先将Y的形状改为(时间步数*批量大小,隐藏单元数)
        # 它的输出形状是(时间步数*批量大小,词表大小)。
        output = self.linear(Y.reshape((-1, Y.shape[-1])))
        return output, state

    def begin_state(self, device, batch_size=1):
        if not isinstance(self.rnn, nn.LSTM):
            # nn.GRU以张量作为隐状态
            return  torch.zeros((self.num_directions * self.rnn.num_layers,
                                 batch_size, self.num_hiddens),
                                device=device)
        else:
            # nn.LSTM以元组作为隐状态
            return (torch.zeros((
                self.num_directions * self.rnn.num_layers,
                batch_size, self.num_hiddens), device=device),
                    torch.zeros((
                        self.num_directions * self.rnn.num_layers,
                        batch_size, self.num_hiddens), device=device))

18 行：隐藏层后面的层需要自己定义
23 行：转化为二维张量，变成 [[8.5 循环神经网络的从零开始实现#^784cba]] 的形状，套用之前的训练函数

2. 训练与预测

与 8.5 循环神经网络的从零开始实现类似

device = d2l.try_gpu()
net = RNNModel(rnn_layer, vocab_size=len(vocab))
net = net.to(device)

num_epochs, lr = 500, 1
d2l.train_ch8(net, train_iter, vocab, lr, num_epochs, device)

perplexity 1.3, 404413.8 tokens/sec on cuda:0
time travellerit would be remarkably convenient for the historia
travellery of il the hise fupt might and st was it loflers

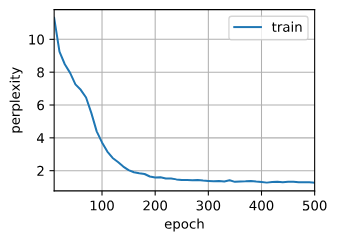
利用框架，训练速度快很多

1. 定义模型

2. 训练与预测

参考文献